Important: Brevity disclaimer.

Intro

The curvature notion plays very important role in differential geometry and it’s often the case that it’s desirable to calculate some approximation for surface curvature in discrete geometry also. Typical applications for this algorithm include:

• Feature recognitions based on curvature: for example, recognition of roundings.
• Visualizations for the user for better understanding of surface properties.
• Some more complex algorithms can use curvature estimation to accomplish their tasks.

However, the notion of curvature is not that easy transferable to discrete geometry - there are a lot of factors that make this transition quite difficult, such as strong influence of triangles shapes and sizes to estimated result or high sensitivity to noise.

I’ve implemented several different algorithms for curvature estimation, results of the latest one were quite good compared to existing and well-known algorithms - please see below for comparisons.

Curvature estimation for BallJoint model

Model is courtesy of Cyberware, Inc.

Curvature Estimation based on discrete differential geometry

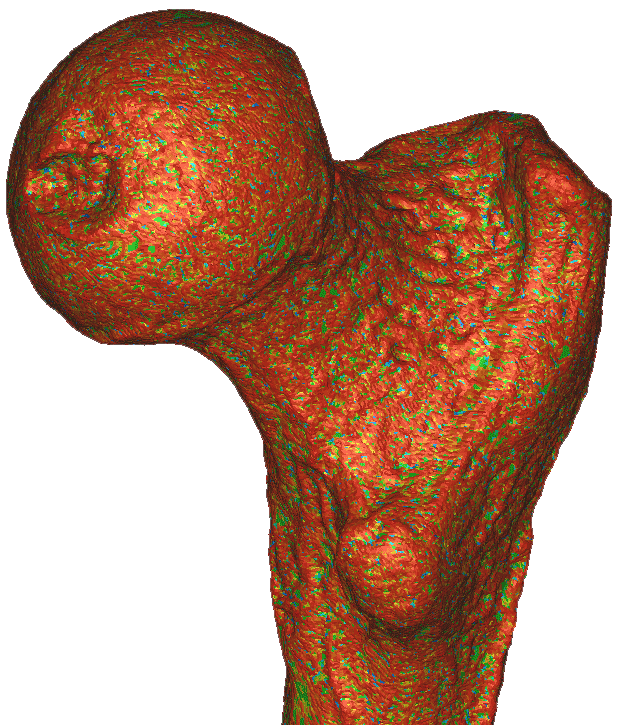
These results were obtained using algorithm described in article Discrete Differential-Geometry Operators for Triangulated 2-Manifolds. It can be seen that due to the noise amplitude comparable to triangles size results are completely random.

New algorithm

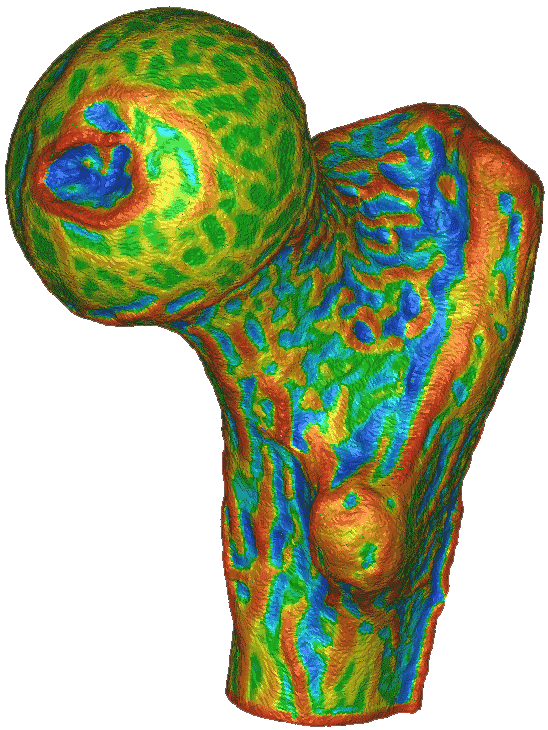
It can be seen that with the new algorithm the curvature can be estimated reliably even for such a noisy model.